HPC tailored solvers in MoFEM

High-Performance Computing (HPC) Optimized Solvers in MoFEM

At MoFEM, significant effort is devoted to implementing algorithms that solve multi-physics problems for solving large scale complex problems. These are essential for creating scalable solvers that maximize HPC resources efficiency, an imperative for the upcoming exascale computing era. The block structure of MoFEM facilitates the use of scalable Krylov solvers and off-the-shelf scalable preconditioners such as multigrid, additive Schwarz method, and block-Jacobi, among others.

The generic data structures in MoFEM are tailored to power efficient block solvers, providing practical, hands-on examples to tackle real-world problems.

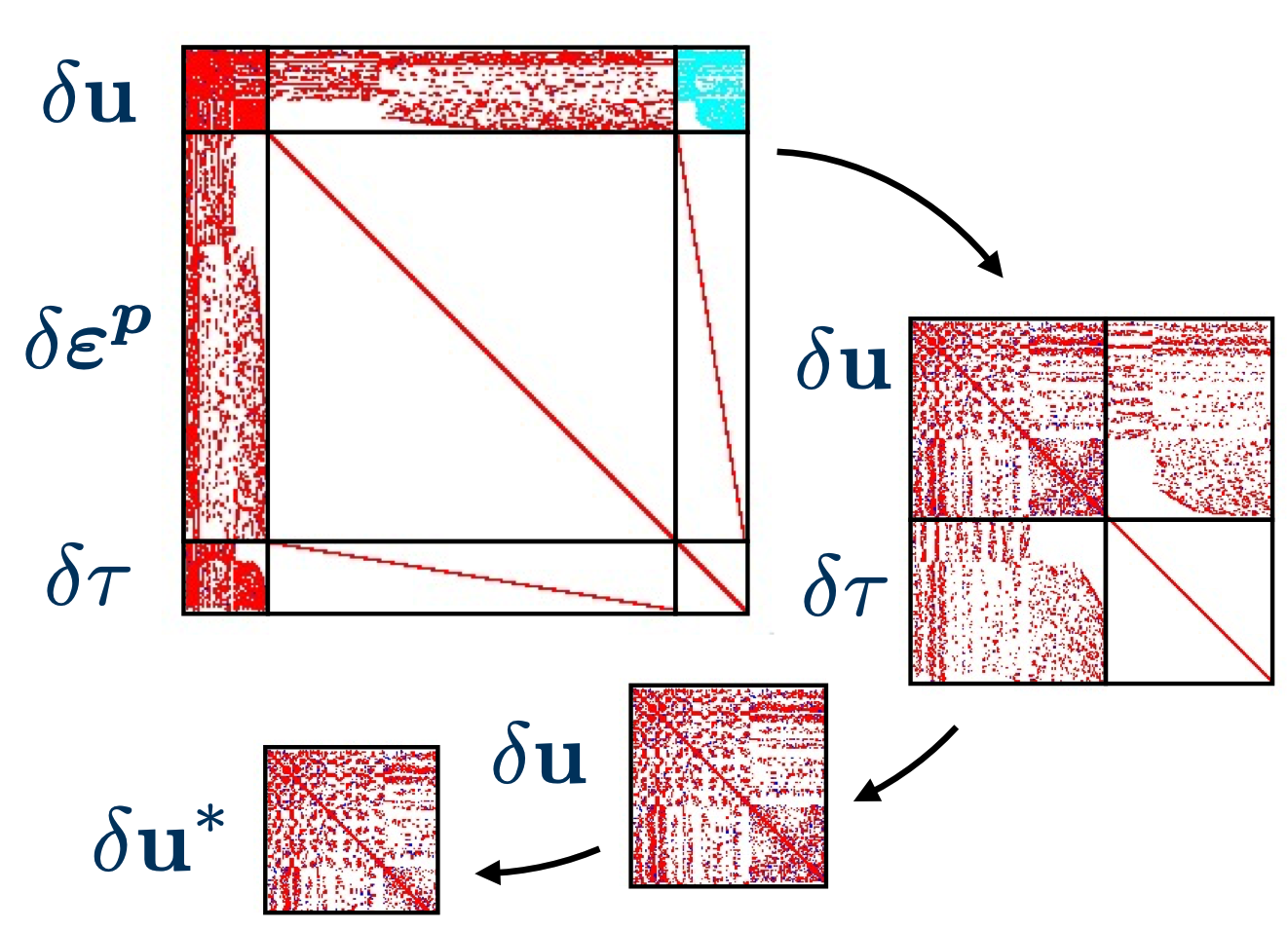
MoFEM’s versatility also extends to the integration of GPU accelerators, allowing for:

• Matrix-free methods that significantly reduce memory bandwidth while increasing floating point operations (FLOPs).
• An architecture that aligns with modern HPC infrastructures, especially those utilizing accelerated hardware.
• A cost-effective computation per degree of freedom (DoF) by combining matrix-free and high-order methods, surpassing traditional low-order methods.

A pilot study demonstrated considerable promise, particularly in problem classes that benefit from matrix-free methods like multifield plasticity.

Below one can find interesting materials regarding HPC optimisations:

• Lectures on performance optimisations
• Data locality
• Small overview on single node optimisations for HPC
• Cachegrind tool tutorial